STATUS: stable Contains functions used for wavelet-based signal denoising. More...
#include "definitions.h"#include <gsl/gsl_wavelet.h>#include <gsl/gsl_rng.h>#include <gsl/gsl_randist.h>#include "eeg.h"
Go to the source code of this file.
Data Structures | |
| struct | WaveletParameters |
| parameters for wavelet-filtering. More... | |
Typedefs | |
| typedef double *(* | SignalExtensionFunction )(double *, int, int) |
| function for extending the signal | |
| typedef double(* | ThresholdFunction )(double, double) |
| function for thresholding. | |
| typedef double(* | ThresholdSelectionFunction )(const double *, int) |
| function for threshold selection. | |
Functions | |
| double | conventional_thresholding (const double *data, int n) |
| Wavelet estimation of single trial ERP's using a conventional estimate. | |
| EEG * | eeg_wavelet_denoise (EEG *eeg, WaveletParameters P, bool alloc) |
| Extend data to length 2^j using sigextfct and denoise it. | |
| double | hard_thresholding (double d, double lambda) |
| hard-thresholding. | |
| double | heuristic_sure (const double *data, int n) |
| thresholding as proposed in the Matlab Wavelet-Toolbox. | |
| double | soft_thresholding (double d, double lambda) |
| soft-thresholding. | |
| double | sureshrink (const double *data, int n) |
| procedure described in Donoho et al., 1995. | |
| double | translation_invariant_thresholding (const double *data, int n) |
| Wavelet estimation of single trial ERP's using Wang et al.'s (2007) technique. | |
| int | wavelet_denoise (double *data, int n, WaveletParameters P) |
| Generic Wavelet-Denoising. | |
| int | wavelet_extend_and_denoise (double *data, int n, WaveletParameters P) |
| Extend data to length 2^j using sigextfct and denoise it. | |
| WaveletParameters | wavelet_init () |
| set default parameters for a waveletParameters struct. | |
Detailed Description
STATUS: stable Contains functions used for wavelet-based signal denoising.
Wavelet-based signal denoising.
Wavelet Theory
Similar to the Fourier transform, which decomposes a function into bases of sines and cosines, the wavelet transform can be used to obtain a different representation of a function. Unlike the Fourier transform however, the wavelet transform is not limited to specific functions, but rather decomposes a function into bases of scaled and shifted functions of a mother function, commonly referred to as the mother wavelet. Due to the fact that the used mother wavelets are well localized in frequency and time (unlike the sines and cosines used in the Fourier transform), a much more compact and sparse representation of the function can be achieved using wavelets.
Technically, the wavelets are scaled and shifted versions of a function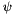
![\[ \psi_{a,b}(t) = \frac{1}{\sqrt{a}}\psi\left(\frac{t-b}{a}\right) \]](form_93.png)
and the continuous wavelet transform (CWT) is characterised by
![\[ \mathcal{W} s(a,b) = \int_{-\infty}^{+\infty}s(t)\psi_{a,b}(t)dt \]](form_94.png)
where s is the signal to be decomposed. Restrictions put on the mother wavelet involve its square and absolute integrability as well as the requirement that the function integrates to 0, thus ensuring a tight localisation in time and frequency space.
In order to overcome the redundancy present in this reconstruction of the function, as well as to make the transform applicable to practical problems, the discrete wavelet transform (DWT) has been developed:
![\[ \mathcal{W} s(j,k) = \frac{1}{\sqrt{2^j}}\int_{-\infty}^{+\infty}s(t)\psi\left(\frac{t-k}{2^j}\right)dt \]](form_95.png)
where j and k are integers.
It has been shown [Daubechies1992] that a function can be reproduced accurately, if and only if the energy of the wavelet coefficients lies between two positive bounds. It can be shown, that the discrete wavelet transform for a discrete signal is equivalent to passing the signal through a filter bank, filtering and downsampling the signal in successive steps to obtain wavelet coefficients at different resolution levels [Jansen2001]. This procedure can be implemented in an efficient way (O(n)) using a pyramidal algorithm, the fast discrete wavelet transform (FDWT) as described in [Press1992].
Wavelet-based Denoising
test test test
Definition in file wavelet.h.
 1.7.0
1.7.0