STATUS: unstable Regularization matrices. More...
#include "mathadd.h"#include "definitions.h"#include "array.h"
Go to the source code of this file.
Functions | |
| Array * | regularization_gaussian_corridor (const Array *points, uint dims[2], Array *m, double max_sigma) |
| Calculate a ''gaussian corridor''. | |
| Array * | regularization_linear_points (const Array *points, uint dims[2], Array *m) |
| Calculate a regularization function that is the distance transform of the piecwise linear interpolation between points. | |
Detailed Description
STATUS: unstable Regularization matrices.
Definition in file regularization.h.
Function Documentation
| Array* regularization_gaussian_corridor | ( | const Array * | points, | |
| uint | dims[2], | |||
| Array * | m, | |||
| double | max_sigma | |||
| ) |
Calculate a ''gaussian corridor''.
![\[ G_f(x,y; \sigma) = \frac{1}{\sigma 2\pi} \exp{\left( -\frac{\min_{\xi}\sqrt{(\xi-x)^2+(y-f(\xi))^2}}{2\sigma^2} \right)} \]](form_61.png)
where $f$ is piecwise linear (approximated with bresenham-alg) and the minimization is approximated with distance-transform (deadreckoning).
- Todo:
- there are artifacts here, check for numerical errors
Example:

- Note:
- if you don't pass any arguments, the regularization is done along the main diagonal
- Parameters:
-
points defining the piecewise linear function through the regularization matrix; this is a 2 x M dimensional INT-array, all points must be within the dimensions; if NULL is passed, the function assumes (0,0),(dims[0]-1,dims[1]-1) as points, i.e. the regularization is done along the main diagonal dims the dimensions of the output matrix (rows x cols) m the output matrix or NULL -> allocate in function max_sigma the regularization parameter
- Returns:
- the regularization matrix or NULL (error)
Definition at line 127 of file regularization.c.
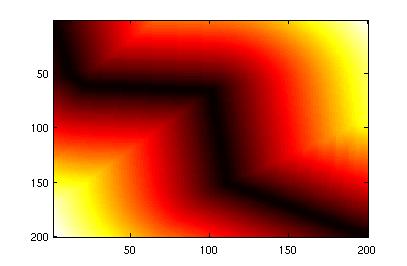
Calculate a regularization function that is the distance transform of the piecwise linear interpolation between points.
(approximated with bresenham-alg). This is a linear fall-off away from the line passing through all points. This function is used e.g. to construct a regularization matrix that punishes deviations from time-markers (stimulus onset, response onset etc).
Example:
- Note:
- if you don't pass any arguments, the regularization is done along the main diagonal
- Parameters:
-
points defining the piecewise linear function through the regularization matrix; this is a 2 x M dimensional INT-array, all points must be within the dimensions; if NULL is passed, the function assumes (0,0),(dims[0]-1,dims[1]-1) as points, i.e. the regularization is done along the main diagonal dims the dimensions of the output matrix (rows x cols) m the output matrix or NULL -> allocate in function
- Returns:
- the regularization matrix or NULL (error)
Definition at line 50 of file regularization.c.
 1.7.0
1.7.0