libeegtools: Dynamic Time Warping

General DTW

Generally, DTW is used to compare or transform two curves such that the difference in temporal characteristics is minimized. It was developed for cases in which there is a general shape in the curves, but they are differently aligned on the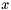 $x$ -axis. First, a pointwise dissimilarity measure between two signals 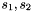$s_1,s_2$ is defined, such as

$d(s_2(t_1), s_2(t_2)) := |\tilde{s_1}(t_1) - \tilde{s_2}(t_2)| + |\tilde{s_1}'(t_1) - \tilde{s_2}'(t_2)|$

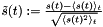where $\tilde{s}(t) := \frac{s(t) - \langle s(t) \rangle_t}{\sqrt{\langle s(t)^2 \rangle_t}}$ denotes the {normalized} signal and 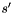$s'$ is the first derivative of 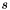$s$ . The data is normalized to find the best match regardless of absolute amplitude, since only the temporal difference between the signals is of interest. The distance used here is referred to as derivative DTW because it considers both amplitude and slope of the signals.

This measure constitutes the dissimilarity matrix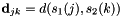 $\mathbf{d}_{jk}=d(s_1(j), s_2(k))$ . An optimal time-mapping according to the metric chosen above is produced by finding a path 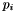$p_i$ that is described recursively by

$\mbox{if } p_i=(j,k) \mbox{ then } p_{i+1} \in \left\{(j+1, k), (j, k+1), (j+1, k+1)\right\}$

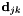through $\mathbf{d}_{jk}$ from the top left to the bottom right corner that minimizes the sum of the $d_{jk}$ .

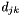This path can be found by a dynamic programming strategy, computing the cumulated cost matrix

$D_{jk} = \mathbf{d}_{jk}+\min{\{D_{j,k-1}, D_{j-1,k}, D_{j-1, k-1}\}}$

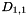and backtracking via the minimum of the three neighboring entries (down, down-right, right) from $D_{J,K}$ to $D_{1,1}$ . The final element $D_{J,K}$ constitutes a measure for the (dis-)similarity of the two curves based on their overall shape. Once this path is available, it is easy to average the curves (called {averaging dynamic time-warping}, ADTW) to reduce both temporal and scale variance by setting

$ADTW\{s_1,s_2\}(t) = \frac{s_1(j)+s_2(k)}{2},$

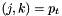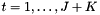where $(j,k)= p_t$ as introduced in Eq. and $t = 1,\ldots,J+K$ .

For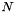 $N$ trials, a straightforward solution proposed in Picton (1988) is to simply combine pairs of single-trial ERPs using ADTW. In a next step, pairs of the results from this combination can be averaged again and the entire process iterated until only one average is left. Recursively,

$ADTW\{s_1,\ldots,s_{2N}\}(t) = ADTW\{ADTW\{s_1,\ldots,s_{N}\}, ADTW\{s_{N+1},\ldots,s_{2N}\}\}(t)$

with base case from Eq..

Dynamic Time Warping

General DTW

Integration of additional time-markers